THE OPPOSITE OF ILLUMINATION
Why is the fear of scientists not told? Why is the doubt that is part of the very subject of scientific articles systematically omitted? Why are the dark spots that surround the most fundamental discoveries always masked?
We like to present science as the temple of reason. Everything would be clear here. Everything here would make sense. Here, everything would be clean and burr-free. That may be true in mathematics. This is certainly not the case in other scientific disciplines. Why? Why? Because scientists are confronted with new ideas that emerge from their investigations, like children see a clown mounted on a spring gushing out of a box they have opened without asking their parents. Like these children, scientists are afraid. Like them, they doubt what they see. Like them, they stammer at the first words they hear. Those words are weak. They’re unsuitable. They’re anything but fair.
I would like to illustrate my point with three examples: the discovery of energy quantification by Max Planck, the discovery of the so-called “uncertainty principle” by Werner Heisenberg, the discovery of the fundamental equation of elementary particle motion by Erwin Schrödinger.
1 | Case study n°1 : and fear becomes a fundamental constant in physics
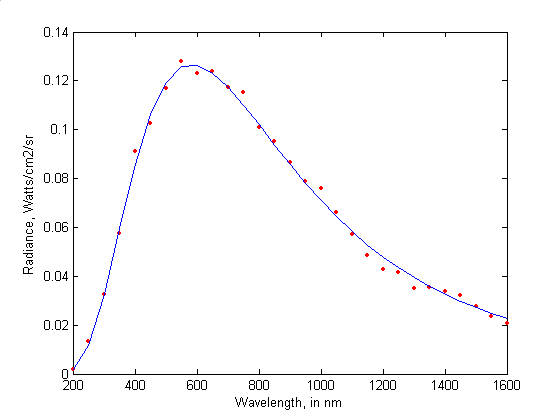
Fig 1: The radiation spectrum of the black body (©Tom O’Haver)
The curve in Figure 1 represents the spectrum radiated by the black body. What does that mean? Heat a piece of metal, it glows: it emits light. For a physicist, light is always plural. They are lights, of all colours, even if our eyes would melt them into a single resultant, and our language would have only one word: red, orange or white.
The catalogue of all emitted lights is called a spectrum. It takes the form of a curve whose each point represents an intensity in the set of possible shades of colors, which are infinite in number. To observe the color of a piece of metal that heats up is to draw the curve of the spectrum of the emitted light.
At the end of the nineteenth century, the question of the radiation of a piece of metal is a problem that intrigues physicists. Yet the experimental protocol is elementary. The metal sample is enclosed in a perfectly closed, and therefore black, chamber that has been drilled with a microscopic hole. This enclosure and its contents represent the black body. We observe the light that escapes while varying the temperature. But if the protocol is elementary, the light intensity curve defies all explanations.
In 1893, the German physicist Wilhelm Wien proposed a law which gives a very good account of the left part of the radiation curve: the rapid rise. Unfortunately, this law is in contradiction with what we observe in the part on the right: the slow descent.
Conversely, two other English physicists, John Rayleigh and James Jeans, have established a law which fits very well with measurements to the right of the spectrum, but fails to explain the left part of the curve. It’s a dead end. No one has a satisfactory interpretation.
And for good reason, this curve does not belong to the continent of classical physics. It is like a debris made of a strange material that would have washed up on a beach, or a meteor. It belongs to another world, still unknown at that time, that of quantum physics.
When the German physicist Maxim Planck stood up and advanced before his colleagues at the Berlin Physical Society on Friday 14 December 1900, it was to deliver a paper which he entitled Über das Gesetz der Energieverteilung im Normalspectrum[1] (On the theory of the law of the distribution of energy from the normal spectrum). In this paper, he will set out the theoretical solution to this problem. It holds in few words: energy is not a continuous variable, it is quantified. It comes in tiny packages. From the quantification of energy derives the shape of the entire spectrum emitted by the black body.
The moment of this communication is that, very precise, of the foundation of quantum physics. But this is not a moment of glory as we usually represent it. For Max Planck, the solution he enunciates remains a sort of mystery. It is so unthinkable that he does not see it. He doesn’t recognize her for who she is.
That’s why Max Planck brought back a simple calculation device that day. This one allows, he explains, a little embarrassed, to reproduce entirely the curve of the spectrum of the black body, in a rather incongruous way, he insists, but at the same time sufficiently precise that he felt the need to share this result. In the ensuing debate, Max Planck refuses to give any meaning to this calculation device. The truth is, what he found scares him.
In Planck’s original communication, the energy quantum appears as a constant which he names h. This is the fundamental constant of quantum physics. Later, he will tell that this letter was put for “Hilfe!” Help! Help!
What did Max Planck see when he discovered quantum mechanics? What image formed at the bottom of his pupil at that moment, of which he conceived a violent fear as irrepressible as it was instantaneous? He saw something monstrous suddenly appear, as a clown leaves his box, without warning.
One might think that his discovery for Max Planck as an illumination. It’s just the opposite. The darkness fell upon him. It will take years of hindsight, and Albert Einstein’s help, for him to understand the true scope of his communication.
We are taught that a discovery would always occur, at the moment it occurs, in such a crystalline limpidity that it would instantly acquire an obvious character. It is the image of the light bulb that lights up, and the light suddenly spreads. This image is simply false.
2 | Case study n°2 : The so-called “Heisenberg uncertainty principle”: three words, two errors.
The fundamental constants of physics are not the only ones to keep track of the mental confusion that occurs in the brain of the discoverer, at the moment he discovers. There are also the words. There are expressions. Maybe there’s all the language, if we can date it. This is the case of the so-called “Heisenberg uncertainty principle”: three words, two errors.
As we know from Louis de Broglie’s work, we observe an essential duality, at the most fundamental level, between a particle and a wave, that is, a vibration. These are two sides of the same coin. This duality works like a match. Any vibration can be associated with a particle whose energy is derived from the measurement of frequency, and vice versa. The question Werner Heisenberg explored in January 1927 is this: what happens if the wave is not infinite, as we usually think, but finite, as it always is?
This situation raises a mathematical problem of very silly appearance. In the case of a finite wave, the frequency cannot be measured with absolute precision. Words are important: it is not that we do not know (a problem of uncertainty), it is that we cannot (a problem of indeterminacy).
We can understand that simply. Frequency is the number of beats of the wave divided by its duration. The numerator (the number of beats) is an integer that changes incrementally, while the denominator (the duration) is a real number. It is a quantity that evolves continuously, by infinitesimal values.
For an infinite wave, this does not pose any particular problem. The frequency is unambiguously defined. For a finite wave, on the other hand, we find an interval of durations that correspond to the same number of beats. In practice, this interval is small, but it has an unfortunate consequence: the definition of the frequency is then tainted with uncertainty.
If there are several possible durations for the same number of beats, then there are several possible frequency values. This uncertainty is irreducible. Frequency is a concept that only makes sense for an infinite wave.
The result Heisenberg finds when he transposes this problem in the case of a particle is difficult to understand. Its conclusions are paradoxical. The details of what would commonly be called “position” and “velocity” of the particle are related. Concretely, the more you seek to know the extension of the particle, the less you know precisely what its speed is, and vice versa.
This is not a principle, but a demonstrable result. It is not uncertainty but indeterminacy. Yet Werner Heisenberg does not understand it this way.
In his original article Uber den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik[2] (About the intelligible content of kinematic theory and quantum mechanics), he uses the term “ungenauigkeit” (uncertainty) thirty times to describe what he found. It will take a little distance for him to understand that it is a property of indetermination (“unbestimmtheit”). Thus this initial confusion will continue even in the everyday language of scientists, in the same way, and for the same reason, that the native American inhabitants are still called “Indians”.
3 | Case study n°3 : the discovery of the fundamental equation of elementary particles
Erwin Schrödinger made one of the major discoveries of the 20th century in physics. The equation that now bears his name is the equivalent for the elementary particles of Newton’s equation for classical mechanics.
The original article dates from 3 September 1926[3]. Schrödinger’s reasoning in this text is simple to describe. If particles behave like waves, as Louis de Broglie showed two years earlier, then these particles should obey a wave equation.
Not only did Erwin Schrödinger succeed in writing this equation, but he solved it in the case of an electron subjected to the attraction of a proton. In doing so, he demonstrates through theory a fundamental result that until then existed only in an experimental form: the energy levels of the atom are quantified. Erwin Schrödinger thus finds the spectrum of the hydrogen atom by calculation.
“A moving particle is nothing more than the foam that appears on the radiative waves that form the matter of the world,” he wrote. But how to describe this foam?
In the case of Newton’s equation, the fundamental observable, we know, is the position of moving matter. Solving Newton’s equation means finding the evolution of the position of matter under the influence of surrounding forces.
But what is the fundamental observable in the case of the Schrödinger equation? What are these waves that describe the quantum world? When he published his article, Erwin Schrödinger did not name this wave. He associates a mathematical symbol with it, y. Its interpretation is as follows: it describes the distribution of the charge of the electron.
But this interpretation is wrong. She will be discredited very soon.
When Erwin Schrödinger published one of the most important scientific discoveries of his century, he simply did not know what he had understood. He is struck with blindness before his discovery.
The question is so fundamental to physics that it will immediately mobilize the entire community, in the form of fierce debates, some of which have become legendary. These debates will last for years. They will separate men into schools of thought. They’ll bounce back multiple times. They may not even be finished yet.
From the point of view of the novelty production process, no matter what response persists (this wave represents the probability density of the particle’s presence in the space of the configurations), and which gave it its final turn (Max Born). The main thing is elsewhere. Not only did the innovator not find the meaning of what he had brought to the world, but that meaning did not exist in the original article he published.
4 | Discovery versus invention
This fear, this babbling, these maladjusted words are part of science. They do not take anything away from the greatness of these stories of discovery. Quite the contrary. In my view, they are additional evidence of the fundamental difficulty of searching the unknown. They are all scars of the struggle of men against darkness that have become inscribed in history and language. Then why do our teachers ignore them? Why don’t scientists tell us about science in its human reality? I see three explanations. Each of these explanations refers to a duality. They are: discovery versus invention, science versus politics and science versus art.
Scientists see themselves as discoverers of reality. Words are important.” Discovering” is literally uncovering: removing a blanket. At the heart of science is the idea that every discovery exists at the time it was made. The researcher reveals reality, that’s all. His only merit is to lift the fabric that prevents our eyes from seeing what he found, which was there from all eternity, waiting for the light. In this sense, scientists would oppose inventors. Inventors are those who make a new reality emerge. The result of their work, What they do, does not pre-exist when they do it. Like artists, inventors create from scratch the reality they offer to see.
Of course, it is more complicated than that, for at least two reasons. The first reason is the functioning of our brain. The second is language.
First, our brains are built on a particular world view. Any deviation from this design requires neural reconfiguration. This reconfiguration is not abstract, it is physical: neurons that were not connected until now must connect. It’s a job comparable to making a new reality.” To understand is to create,” wrote Albert Camus.
In his book Against the Method, Paul Feyerabend goes even further in this reflection. It shows that what was initially not rational in science becomes rational slowly, as usual: “Theories only become clear and’reasonable’ after prolonged use of their incoherent parts. Such a precondition, absurd, unreasonable and not methodical, then becomes an inevitable precondition for clarity and empirical success.
Secondly, language is essential. The scientist may try to be rational, but the words he uses do not belong to him. These are words that others have shaped to describe their reality. Faced with a completely different reality, they are dumb, in the etymological sense: weak. That is why the scientist who discovers something radically new must invent words to describe his discovery. From that moment on, his discovery is no longer a discovery. It becomes the invention of words to say it.
Boileau wrote: “What is well conceived is clearly stated, and the words to say it come easily. All the stories of the discoverers, all the history of inventions, all the situations where one faces the unknown show that Boileau is wrong. What is absolutely new can never be well conceived, and it cannot be stated clearly, and the words to say it have yet to be invented. Whoever looks reality in the face sees a sphinx[4].
It is not uninteresting to note that the myth of enlightenment is a myth specific to discoverers. Only discoverers can imagine that a light suddenly came on when they made their discovery. For inventors, this is impossible: not only do they not know what they are doing, but this thing does not pre-exist. Therefore, they cannot recognize it.
5 | Science versus politics
There is a game very well known to creativity professionals, which can quickly get to the root of things. That’s the why game. Someone tells you something: ask them “why?” Once he’s finished his explanation, ask him again, “Why?” And so on, until the true reasons for his actions appear to you in full light.
Why do scientists refuse to mention their fears, their doubts, their babbling? Because they see themselves as discoverers, rather than inventors. Why? Why? At this level of reflection, I believe that the answer implies another duality: science versus politics.
Fear, doubts, stammering, but also sexuality, desire, jealousy: how is it that everything human is systematically excluded from the scientist’s field of consciousness? Perhaps because everything human is also political.
A journalist was surprised one day that Michel Foucault, a scholar, a professor at the Collège de France, the holder of the chair Histoire des systèmes de pensée, began to engage in politics. Michel Foucault replied: “But it is the opposite that should surprise you. Politics is everywhere. It is the silence of the teachers that is suspect, that should ask the question.”
Michel Foucault answered this question in his own way: brilliant, disturbing, inescapable. In the lecture he gave at the Pontifical Catholic University of Rio de Janeiro, Brazil, from 21 to 25 May 1973[5], Michel Foucault demonstrates that scientific investigation derives from judicial investigation, and this history leaves much more than traces in the form of scientific knowledge. He says: “With Plato begins a great Western myth: that there is an antinomy between knowledge and power. If there is, he must give up power. Where knowledge and science lie in their pure truth, there can no longer be political power. This great myth must be liquidated.”
To imagine that one is a discoverer rather than an inventor is to think that one’s work is placed in a dimension of the independent reality of the city: its operating rules, its values, its history. It’s a simple way to get out of politics. It is to exclude from the mental field all that is likely to question the form of power in place. It is to reactivate the great myth of which Michel Foucault spoke: that there is an antinomy between knowledge and power.
6 | science versus art
The separation between art and science is recent in Western history. What has happened since Leonardo da Vinci to make it so strange that a scientist is also an artist, and so suspicious that an artist calls himself a scientist? How to understand the great movement of separation of one from the other from the most elementary school? How can we explain that some of them place themselves in the first ranks of the city, while others experience all the difficulties of the world to live? This is one of the fundamental questions of this research, and therefore of this blog.
In the light of the preceding reflections, one may wonder to what extent the great separation of scientists and artists would not essentially be a distinction in their relationship to power. On the one hand, those who have (explicitly or implicitly) renounced questioning power, questioning its foundations, highlighting its consequences: scientists. On the other hand, those who would continue to criticize society head-on through their works: the artists. Maybe. To be continued…
Miguel Aubouy
Photo credit: ShareGrid Co-Founder, Brent Barbano (unsplash).
1] Planck, M. (1901), Uber das Gesetz der Energieverteilung im Normalspectrum. Ann. Phys. 309: 553-563. doi:10.1002/andp.19013090310
2] Heisenberg, WZ Physik (1927) 43: 172. https://doi.org/10.1007/BF01397280
3] An Undulatory Theory of the Mechanics of Atoms and Molecules, E. Schrödinger, Phys. Rev. 28, 1049 – Published 1 December 1926.
4] Miguel Aubouy, Le syndrome de Vasco de Gama, 2015, les éditions Nullius in Verba.
5] Michel Foucault, Dits et Ecrits, document n° 139
Translated with www.DeepL.com/Translator